为什么加速的观察者在真空中能探测到粒子？最

根据物理学家斯蒂芬·富勒、保罗·戴维斯和 W. G.盎鲁所描述的盎鲁效应，加速观察者的真空似乎是有温度的。换句话说，如果一个观察者在一个加速参照系中，他将探测到粒子，而在一个非加速参照系中，他将探测不到粒子。 图1：加拿大物理学家 W. G.盎鲁，盎鲁效应的共同发现者。匀速运动

让我们考虑一个观察者，比如一个在宇宙飞船里的宇航员，以恒定的加速度在闵可夫斯基时空中运动。二维度规张量η的对应矩阵表示为：

式1：闵可夫斯基时空的度规张量η的矩阵表示。对于c：

式2：二维闵可夫斯基线元。利用固有时间τ参数化观察者的运动，我们得到以下两个条件（第二个条件通过微分第一个得到）：

式3：根据第一个条件（上），将2维速度归一化。第二个条件（下），通过微分第一个得到，说明2维加速度和速度是正交的。加速观察者的视界

一个加速的观察者（受恒定力的影响）以双曲线运动（稍后将会显示）。如下图所示，一个加速的观察者可以超过光线，只要他出发足够提前。因此，他有一个以视界为界的隐藏区域。这类似于黑洞，那里也有一个看不见的区域，边界作为视界。

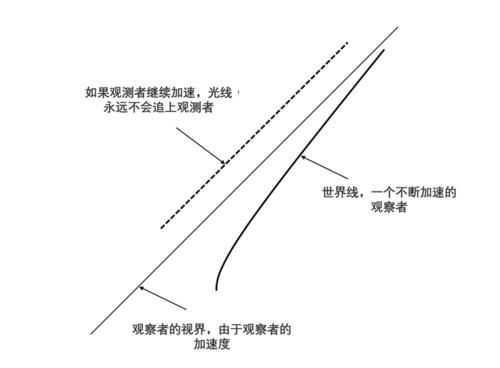
图2：草图显示，只有出发足够提前，一个加速的观察者就可以超过光线。如下面的时空图所示，在t < 0时离开原点x=0的光子A追上了观察者。但是，光子B在t >0处的原点就不会追上观察者了。

图3：显示两个光子A和B的时空图。前者赶上观察者。后者从来没有。由于在瞬时移动的惯性系（附在观察者身上的参照系）中，观察者处于静止状态，我们有：

式4：在瞬时移动的惯性系中，观察者处于静止状态，2维速度为u=(1,0)。请注意，从公式3：

其中a是常数。这在任何惯性系中都适用，因此我们有：

式5：恒定加速度条件，适用于任何惯性参照系。我们的目标是证明一个加速观测者将会探测到粒子的存在，而非加速观测者则探测不到。为了证实这一点，选择一个覆盖闵可夫斯基时空的新坐标是很方便的。这些坐标称为光锥坐标。

光锥坐标

这些坐标根据原始(t,x)定义为：

式6：光锥坐标的定义。闵可夫斯基时空中相应度规张量的矩阵表示为：

式7：闵可夫斯基时空光锥坐标度规张量的矩阵表示。用式7替换式3和式5中的η，得到：

式8：光锥坐标的一阶导数和二阶导数所满足的条件。这些问题很容易解决。经过一些代数操作（包括缩放和坐标原点的移位），我们得到：

式11：在坐标(t,x)中，加速观察者的世界线是一个双曲线。因此，我们得出结论，在t-x坐标系中，加速观察者的世界线是双曲线：

观察者最初在x→∞处移动，静止在x=1/a处，并在途中减速。然后加速回到x→∞。注意当x→∞时，他的轨迹接近光锥。

图4：在t-x坐标系中，加速观察者的世界线是双曲线。观察者最初在x→∞处减速，直到停在x=1/a处。停止后，他加速回到x→∞（注意，当x→∞时，他的轨迹接近光锥，用虚线表示）。共动坐标系（Comoving Frames）

现在让我们为加速观察者找到一个运动坐标系。我们将寻找一个参考系：

当空间分量ξ=0时，观测者处于静止状态时间坐标ξ=τ，观察者的固有时间（沿着他自己的世界线的时间）此外，在共动坐标系中，度规保形平坦是很方便的（当我们把量子力学包括进来时，这将变得很清楚）。根据定义，保角映射是局部保持角度而不一定保持长度的数学函数。

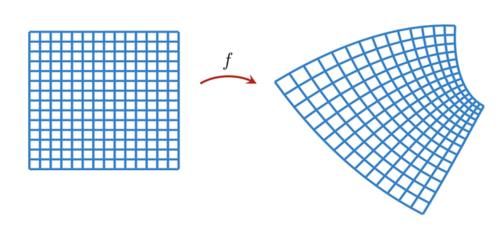
图5：保角映射的示例。在矩形网格（左）和f映射下的图像（右）中，成对的线相交于90°。在保形平面流形中，每一个点都有一个邻域，可以用保形变换映射到平坦空间。因此，共动坐标系中的线元素具有如下形式：

式12：共动坐标系中的线元素。Ω仍未确定。为了找到Ω(ξ，ξ)的表达式，我们首先定义了移动参照系的光锥坐标：

式13：共动参考系中的光锥坐标。为了避免在ds上出现光锥坐标的二次微分，我们必须有以下变量依赖关系：

式14：原光锥坐标与共动坐标系下的光锥坐标的关系。只需几个简单的步骤，就可以快速地推导出式14中函数的实际形式。他们是：

上一篇：乔欣一改乖乖女形象，真空穿黑色皮衣配牛仔裤
下一篇：没有了