真空是一种能量尽可能少的空间。然而，真空并不完全是空的。它包含量子场。量子场是经典场量子化后得到的，经典场是时空坐标的函数（如电磁场）。数学上量子场是空间和时间的算子值函数。

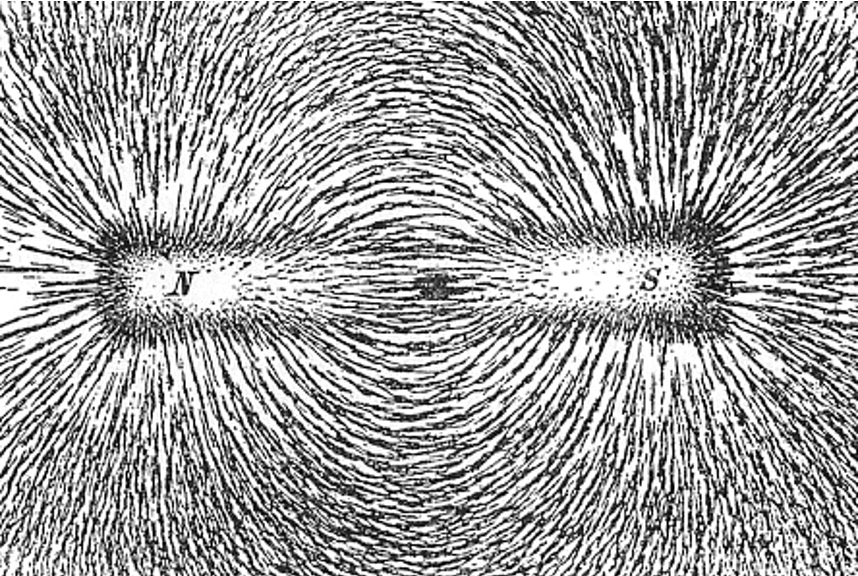
• 图1：将铁屑置于条形磁铁上方，可以看到条形磁铁产生的磁场线。它们按照磁场的方向对齐，形成闭合的线。

有两种类型的真空，一种真正的真空（或真基态），这是一个位于全局势能最小的量子场的稳定构型，另一种是假真空基态，它是占据局部最小值而不是全局最小值的量子场的亚稳定构型。不稳定性是由量子隧穿的势垒穿透造成的（经典场论中，两个真空都是稳定的）。

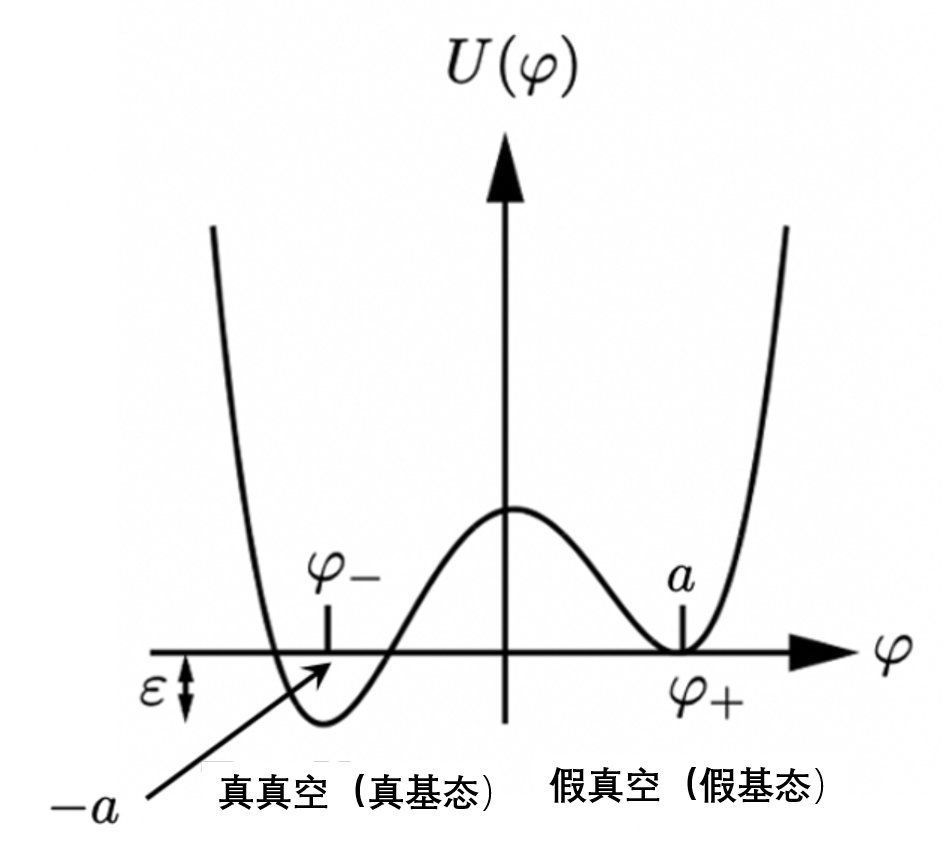
• 图2：含假真空的标量场φ的非对称双阱势（其能量比真真空的能量高ε）。向真真空的转变可以通过量子隧穿实现。

为了方便起见，把假真空选为零。我会解释为什么我们宇宙的真空状态有可能是假的真空。如果是这样的话，它可能会经历一个“隧道”过渡到真正的真空，其后果将是灾难性的。在这个由量子涨落引起的转变过程中，一个真真空的气泡就会形成。如果气泡足够大，它在能量上有利于它的生长和扩散，最终在在整个宇宙中把假真空转化为真真空（真正的宇宙级灾难）。

正如著名的美国理论物理学家西德尼·科尔曼指出的那样，这个概率是非零的，因为我们宇宙的年龄并不是“无限大”（如果是的话，真空衰变早就发生了）。大爆炸之后，宇宙不是任何真空状态（因为它的能量密度是巨大的）。当它冷却时，它可能“选择”了假真空（而不是真真空）。如果想要预测宇宙未来的变化，计算它的衰变概率是至关重要的。引用科尔曼：

• 图3：著名的美国理论物理学家西德尼·科尔曼因其对高能理论物理的贡献而闻名。

因此，我们将计算衰减概率 Γ/V。我们会看到 h的零阶函数是这样的：

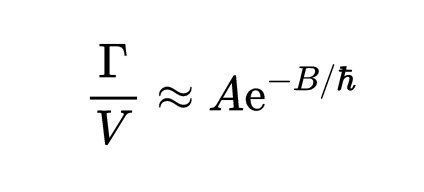
• 式1：单位时间单位体积衰减概率的数学形式。

其中A和B是理论相关系数。

如这篇文章所示：

一个很好的类比，统计物理中的成核过程

在沸腾的过热液体中，也会发生类似的现象。当液体被加热时，它会稳定在一种亚稳态的流动状态（而不是蒸发）。假真空和真真空分别对应于过热的液相和气相。

热涨落（而不是量子涨落，见上文）导致液体中的小气泡不断物化。由于气泡内部是真正的真空（具有较低的能量密度），它的存在降低了系统的总能量。然而，气泡的表面能增加了系统的能量。最终，一个足够大的气泡会物化，这样它就能从能量上促进它的膨胀（相反，小气泡往往会收缩和消失）。然后，它会将可用的液体转化为蒸汽

• 图4：当过热液体开始转变为蒸汽时，气泡形成，这个过程称为气泡成核

粒子的量子隧穿

虽然我们需要量子场来解释宇宙的隧穿，但首先考虑非相对论量子力学中的隧穿是有帮助的。

让我们考虑一个粒子通过的势垒隧穿。这本质上是一种量子现象（经典粒子会反弹）。下图显示了电子波穿过势垒的情形。右边的暗点代表穿过势垒的电子。

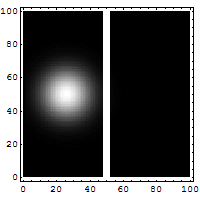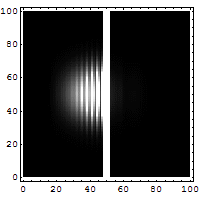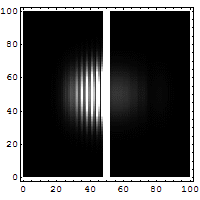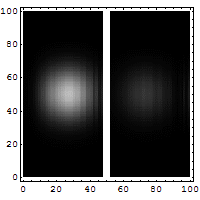
• 图5：电子波穿过势垒

对于总能量为E的粒子，在势为V的区域内（见图6），隧穿速率的形式如下（h为零阶）：

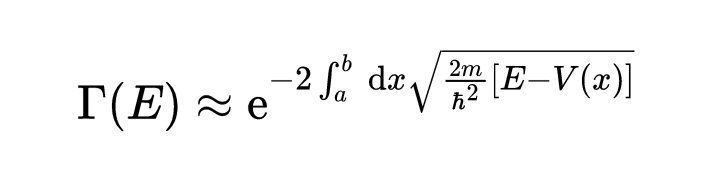
• 式2：图6所示势垒的隧穿速率。

注意，省略了一个前因子。

上一篇：徐璐穿着愈发大胆，穿“真空裙”靠两条细带支
下一篇：没有了